Khi một vật thực hiện 2 dao động điều hoà đồng thời trên cùng một phương, li độ tổng hợp của vật sẽ là sự kết hợp của hai dao động thành phần. Đây là một khái niệm quan trọng trong vật lý, thường xuất hiện trong các bài toán ôn thi. Bài viết này, được chia sẻ trên asanzovietnam.net, sẽ đi sâu phân tích cách xác định phương trình dao động tổng hợp dựa trên đồ thị li độ, giúp bạn hiểu rõ bản chất và phương pháp giải.
Khái niệm Tổng hợp Dao động Điều Hoà
Tổng hợp dao động điều hoà là quá trình tìm li độ, vận tốc, gia tốc tổng hợp của một vật chịu tác dụng đồng thời của nhiều dao động điều hoà cùng phương, cùng tần số. Li độ tổng hợp tại mỗi thời điểm bằng tổng li độ của các dao động thành phần. Kết quả của sự tổng hợp này là một dao động điều hoà mới cùng tần số với các dao động thành phần, nhưng có biên độ và pha ban đầu khác. Việc hiểu rõ cách tổng hợp dao động là nền tảng để giải quyết các bài toán phức tạp hơn về sóng và các hiện tượng vật lý liên quan.
Phân tích Đồ Thị và Xác định Phương Trình Thành Phần
Để tổng hợp dao động điều hoà, bước đầu tiên là xác định phương trình dao động của từng thành phần dựa trên thông tin cho trước, chẳng hạn như đồ thị li độ theo thời gian. Từ đồ thị được cung cấp, chúng ta có thể phân tích đặc điểm của hai dao động x1 và x2. Dao động x1 có biên độ cực đại là 3 cm và bắt đầu từ vị trí cân bằng (li độ bằng 0) theo chiều dương tại thời điểm t=0. Dao động x2 có biên độ cực đại là 1 cm và bắt đầu từ li độ -1 cm (vị trí biên âm) tại thời điểm t=0.
Dựa vào các đặc điểm này, chúng ta có thể viết phương trình cho mỗi dao động. Với x1, xuất phát từ vị trí cân bằng theo chiều dương, pha ban đầu là -π/2. Với biên độ 3 cm, phương trình là x1 = 3 cos(ωt – π/2). Với x2, xuất phát từ vị trí biên âm (-A), pha ban đầu là +π (hoặc -π). Với biên độ 1 cm, phương trình là x2 = 1 cos(ωt + π). Tần số góc ω là như nhau cho cả hai dao động vì chúng cùng thực hiện đồng thời và cùng phương.
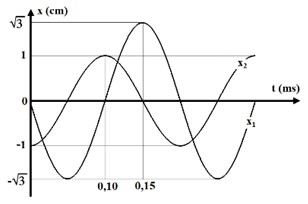Đồ thị li độ x1 và x2 theo thời gian của một vật thực hiện 2 dao động điều hoà
Phương Pháp Tổng Hợp Dao Động bằng Số Phức hoặc Phasor
Phương pháp hiệu quả nhất để tổng hợp hai dao động điều hoà cùng phương, cùng tần số là sử dụng biểu diễn bằng số phức hoặc phasor. Mỗi dao động điều hoà dạng x = A cos(ωt + φ) có thể được biểu diễn bằng một số phức có module bằng biên độ A và argument bằng pha ban đầu φ, tức là A∠φ. Dao động tổng hợp x = x1 + x2 sẽ tương ứng với tổng của hai số phức biểu diễn x1 và x2.
Áp dụng cho bài toán này, dao động x1 = 3 cos(ωt – π/2) được biểu diễn bởi số phức 3∠(-π/2). Dao động x2 = 1 cos(ωt + π) được biểu diễn bởi số phức 1∠π. Để tìm dao động tổng hợp, chúng ta cần tính tổng hai số phức này: (3∠-π/2) + (1∠π). Việc tính toán này có thể thực hiện trực tiếp bằng máy tính bỏ túi có hỗ trợ tính toán số phức ở chế độ cực.
Hướng dẫn sử dụng máy tính tổng hợp 2 dao động điều hoà
Như các bước sử dụng máy tính được trình bày trong bài gốc (chuyển sang chế độ tính toán số phức, nhập 3∠-90° và 1∠180°, nhấn “=” rồi chuyển kết quả sang dạng cực), ta sẽ thu được kết quả là 2∠120°. Lưu ý rằng 120° tương ứng với 2π/3 radian. Kết quả này cho biết dao động tổng hợp có biên độ R = 2 cm và pha ban đầu φ = 120° (hoặc 2π/3 radian).
Kết Quả Dao Động Tổng Hợp
Dựa trên kết quả tổng hợp bằng phương pháp số phức (hoặc phasor) với máy tính, chúng ta thu được biên độ của dao động tổng hợp là R = 2 cm và pha ban đầu là φ = 2π/3 radian. Từ đó, phương trình dao động tổng hợp của vật khi vật thực hiện 2 dao động điều hoà đồng thời là x = R cos(ωt + φ).
Thay các giá trị tìm được vào, ta có phương trình dao động tổng hợp là x = 2 cos(ωt + 2π/3) cm. Phương trình này mô tả hoàn toàn dao động điều hoà mới mà vật thực hiện, với biên độ và pha được xác định từ sự kết hợp của hai dao động thành phần.
Việc xác định phương trình khi một vật thực hiện 2 dao động điều hoà là một kỹ năng cần thiết trong Vật lý phổ thông. Bằng cách phân tích đồ thị li độ của từng dao động thành phần và áp dụng phương pháp tổng hợp dao động bằng số phức hoặc máy tính, chúng ta có thể tìm ra phương trình dao động tổng hợp. Hiểu rõ phương pháp này giúp giải quyết hiệu quả các bài toán liên quan đến sự chồng chất của sóng và dao động. Nắm vững kiến thức này là bước đệm quan trọng để tiếp cận các vấn đề phức tạp hơn.